초딩 3학년
문제라는데
최근 인터넷에 ‘초딩 3학년 문제라는데‘라는 제목으로
1장의 흥미로운 사진이 올라왔네요. 공개된 초딩 3학년 문제라는데
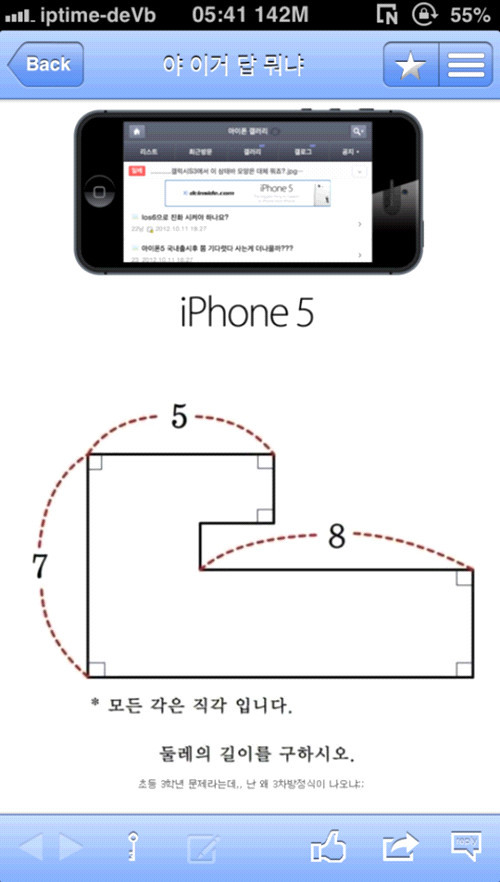
사진 속에는 하나의 도형이 그려져 있고 각변의 길이가 주어져
있는 문제가 담겨져 있는데요.
이 문제는 초등학교 3학년 문제라고 하는데 주어진 각변의 길이를
이용해 전체 둘레의 길이를 구하는 문제네요.
그런데, 초딩 3학년 문제라는데가 왜 이슈가 되고 있는 걸까요?
공개된 게시물을 보면 ‘망할 디씨.. 리플엔 답만 있고 풀이가
없어서 고생했네 ㄱ- 겨우 이해했다 ㅠㅠ 이게 초딩 3학년꺼라니
ㅠ’라는 설명글과 함께 답도 풀이도 없이 문제만 달랑 올라와 있는
모습이 보이는데요.
이건 뭐.., 자기는 답이라도 알고 풀이를 하는데도 고생했다면서
문제만 달랑 올려놓은 저의는 뭔지 궁금해지네요. ㅋㅋ
아마 게시자는 ‘너희들도 이거 푼다고 고생 좀 해봐라’라는 의도로
문제만 달랑 올려놓은 듯 한데요. ㅋㅋ
아무튼 게시자의 의도가 어떻게 되었건 간에 저 역시도 이거
푼다고 조금 고생하긴 했네요. ㅜㅜ
그동안 두뇌개발을 소홀히해서 뇌가 운동부족에 빠졌는지 초딩
3학년 문제라는데 이거 조금 푼다고 뇌가 힘겨워 하면서
헐떡거리는데 아주 미치겠더만요. ㅋㅋㅋㅋㅋ
풀이를 보시기 전에 여러분들도 직접 한번 풀어보세요. 비록
초등학교 3학년 문제라고는 하지만 고생해서 이거 풀고나니 기분은
좋네요. ㅋㅋㅋㅋㅋㅋ
제가 웃는다고 따라서 너무 웃지마세요. 모르긴 몰라도 여러분들
중에서도 답과 풀이를 모른채 풀어본다면 꽤 많은 분들이 문제를
풀다가 포기하실 거라 믿어 의심치 않으니깐요. ㅋㅋㅋㅋ
‘초등 3학년 문제라는데.. 난 왜 3차방정식이 나오냐’라고 말하는
게시자의 말처럼 이 문제를 풀때는 고등수학을 알면 오히려 독이
되는 수가 있어요. ㅋㅋ
풀어보면 아주 간단하고 단순한 문제인데도 오히려 많이 아는 것이
되레 함정이 되어 버리게 만들거든요. ㅋㅋ
딱 초등학생 3학년 수준의 눈높이로 낮춰서 풀면 금방 길이 보이실
겁니다. ㅋㅋ
이 문제는 전체 둘레의 길이를 구하라고 요구하고 있는데요.
일단 기본으로 주어진 값은 세 변의 길이 ‘7, 5, 8’ 뿐입니다.
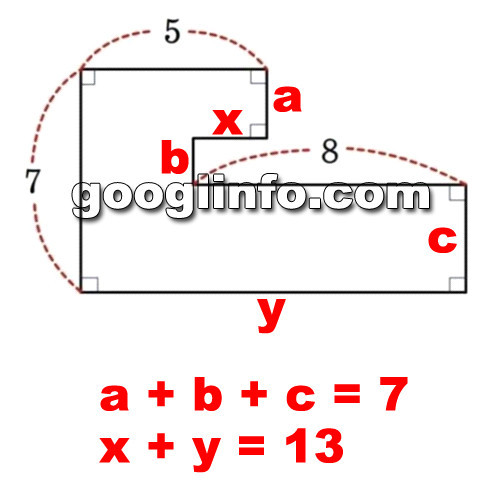
초딩 3학년 눈높이로 생각해보면 전체 길이는 ‘7 + 5 + a + x + b
+ 8 + c + y’가 됩니다.
보기 좋게 정리해보면 ‘a + b + c + x + y + 20’이 되네요.
여기서 우리는 ‘a + b + c’의 값이 ‘7’이라는 것을 금방 유추해 볼
수 있습니다.
그럼 ‘7 + x + y + 20’이 되겠군요.
‘y’는 ‘5 – x + 8’이 되죠? 그럼 ‘x + y’는 간단히 ’13’이라는
답이 나오네요.
고로…., 도형의 전체 둘레의 길이는 ’40’이 되네요. 참 쉽죠~잉?
^^